Abstract

The main target of this paper to show that at certain configuration a Linear Feedback Shift Register yields a maximal length sequence. For simulation and synthesis, FPGAdv 5.2 is used. Also, waveforms and timing are shown.

Keywords: Linear Feedback Shift Register, FPGA, VHDL, Maximal Length Feedback Polynomial.

Introduction

A linear feedback shift register is a combination of series of flip flop and XOR or XNOR logic gates. Its output is pseudo randomly cycle through a sequence of binary values after certain number of clock cycle. The repetition of random output depends on the number of stages in the LFSR. Therefore, it is an important component in communication system where, it play important role in various application such as cryptography application, CRC generator and checker circuit, gold code generator, for generation of pseudorandom sequence, for designing encoder and decoder in different communication channels to ensure network security, Design for Test (DFT) and Built in Self Test design (BIST).

A linear feedback shift register is linear in the sense that its input bit is a linear function (XORing or XNORing) of LFSR previous state. The LFSR feedback in the shift register chain is a function of taps numbers and taps positions. The feedback to LFSR is XOR or XNOR of these taps. However, it is this feedback that causes the random output to start repeating after certain clock cycles. The LFSR works as shift register, if there is no input tap to register bits. An example of 3-bits LFSR is discussed with two different configurations, as shown below is LFSR configured to yield the maximal length feedback polynomial. The input of XOR gate are output of ‘S0’ and ‘S1’ Flip-Flops, and its output is connected as a feedback to the most left register.

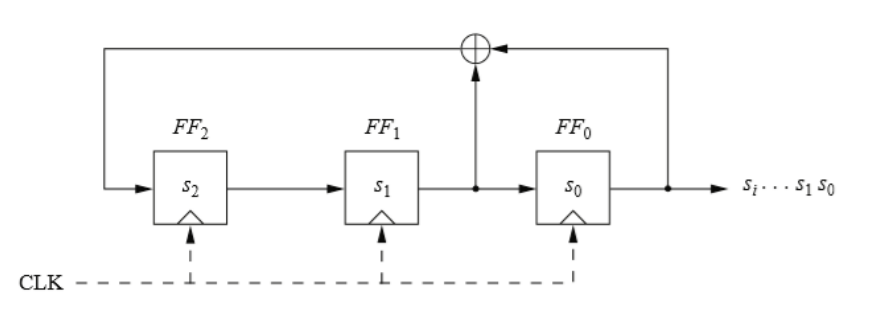Fibonacci implementation of 3-bit LFSR

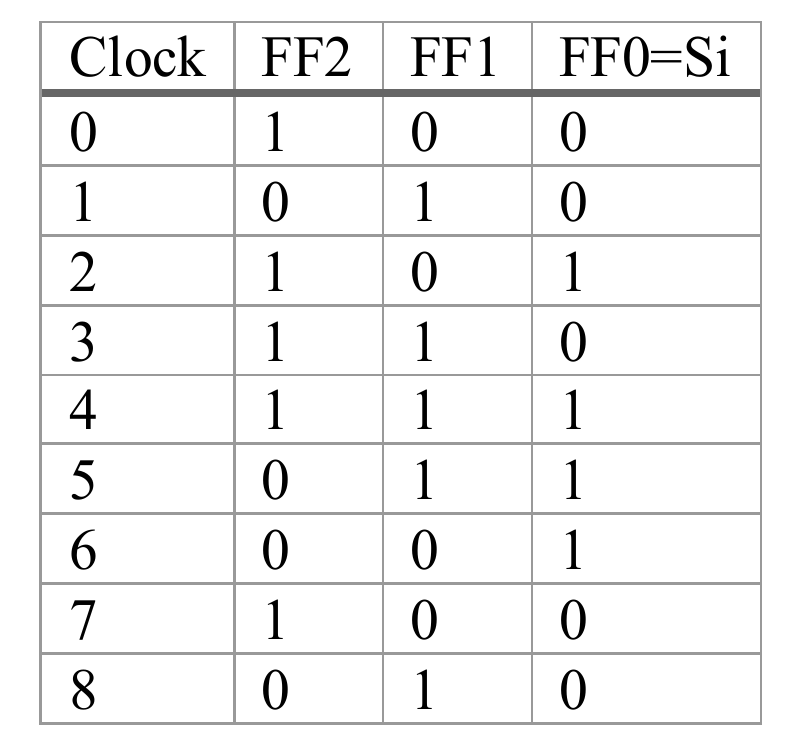Sequence of states of 3-bit LFSR yields maximal length feedback Polynomial

Starting by “100” as a seed value, it will generate random sequence every clock cycle until reach the 7th clock, hence it repeats the previous sequences. But what that means? This LFSR has three D-Flip-Flops. The period at which the sequences are repeated, p = 23 - 1 = 7. Exactly, that number triggers the sequences to be repeated again in the table above. P(x) = x3 + x + 1 is the polynomial representation of this configurations.

The following step discusses the output of another 3-bit LFSR but with different configurations as below. Another XOR gate is connected above ‘S2’ and ‘S1’, hence all feedback taps are activated yielding this polynomial P(x) = x3 + x2 + x + 1 .

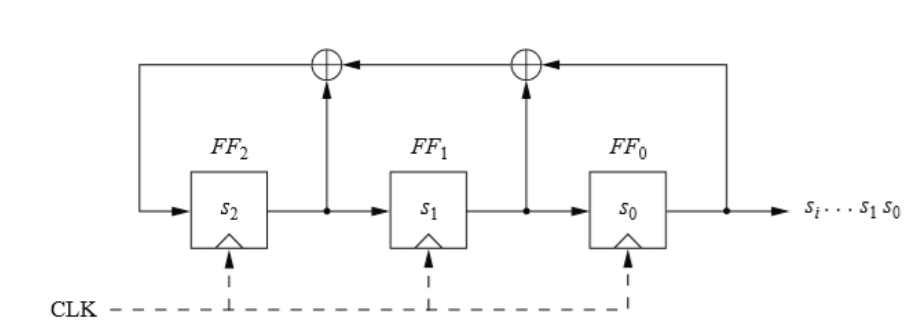another configuration of 3-bit LFSR

Simulation

Simulation of the 1st LFSR configuration

By supplying clock of 50 % duty cycle and 100 ns time period of one cycle. As the reset signal is high, output is the same as the supplied seed “100” at the most first step. When reset goes low, output changes synchronously with the clock’s rising edge.

As shown, at the time 100 reset goes low, the output changes to “010” generating different values at each cycle until reach the time 700, it begins to repeats again. After counting these cycle, we have the number 7 as the maximal length of output sequence, which practical guarantees the previous theoretical demonstration.

Simulation of the 2nd configuration

Counting the clock cycles like above, it yields only 4 cycles, so this configuration only generates only four unique sequences before the sequences repeated again.

Primitive polynomials for maximum-length LFSRs

In our case, (0, 1, 3) is the configuration as listed in the most left second row in the table above.

Conclusion

In this paper, I have shown the implementation of Linear Feedback Shift Register in VHDL, and that at certain configurations, the LFSR yields the maximal length feedback polynomial. The goal of seeking for the maximal length, is making the most benefit of the current hardware and make it much powerful to be included in many application in cryptography or other.

References

[1] Paar, C., & Pelzl, J. (2009). Understanding cryptography: a textbook for students and practitioners. Springer Science & Business Media.